Блог
Финансовая математика “для чайников”, о роли сложного процента
Сегодня будет продолжен, начатый мной статьей про фундаментальный анализ, цикл статей про личные финансы.
Сегодня поговорим про проценты.
Невозможно инвестировать не понимая, что такое процент и как считается доходность.
С простыми процентами как правило проблем не бывает, каждый кто хоть раз держал деньги на депозите в банке понимает, что, например, ставка процента 10% годовых на вклад 50 000 руб. даст 5000 дохода за год.
Сложнее понять действие сложного процента, а он очень важен именно в долгосрочном инвестировании, т.е. когда инвестиции делаются с целью обеспечения финансовой свободы.
По сути при сложном проценте процентный доход вновь инвестируется, увеличивая размер вклада. Вот пример, допустим у вас есть 100 000 руб. и на них Вы получаете 10% дохода, т.е. 10 000 руб. в год.
В первый год Вы получили 10000 руб. и Ваш вклад увеличился на эти 10 000 составив 110 000 руб.
Во второй год Ваш доход уже составит 10% от 110 000 руб., т.е. 11000 руб., которые Вы также добавляете к вкладу, который становится уже 110 000 + 11 000 = 121 000 руб.
Третий год: Ваша 121 тысяча рублей приносит опять 10%, что в рублях 12100 руб., а Ваш вклад в конце третьего года составит 121 000 + 12100=133 100 руб.
И т.д.
В формализованном виде сложные проценты записываются так:
FV = PV (1 + r) ^ n
где FV – будущая стоимость вклада; PV – начальная стоимость вклада; r – ставка дохода (доходность); n – число периодов.
Ну проверьте формулу на нашем примере FV = 10000 (1 + 0,1)^3 = 133 100 руб. Как видите все сошлось 🙂
Когда Вы инвестируете на долгие сроки, тогда значение сложных процентов возрастает очень сильно.
Представьте себе такой пример, если молоко будет дорожать на 10% в год, сколько оно будет стоить через 20 лет? Если сегодня молоко стоит 30 рублей за литр, то допуская рост стоимости молока на 10% в год, через 20 лет молоко будет стоить FV = 30 (1+0,1)^20 = 201 рубль 82 копейки!
Этот пример кстати говоря очень хорошо показывает необходимость инвестирования, сохранения своих капиталов, так как они обесцениваются так же по формуле сложных процентов.
Эту формулу еще называют “формула Ротшильда”, “формула дьявола”, а на английском и в финансовых кругах это называется “компаундинг”.
Все на земле меняется по формуле сложных процентов: инфляция, рост потребления нефти или пшеницы, меняется население земли и т.д.
Когда Вы инвестируете процент работает за Вас, вот пример я раньше приводил по поводу пенсий:
Какую же сумму удастся накопить среднестатистическому россиянину, если он будет инвестировать по 3000 руб. в месяц в течение 30 лет? Предположим, что рост его инвестиций составит 5% в год, а доходность инвестиций будет равна 17% годовых.
Через 30 лет накопится 32 022 812 руб. Так сложный процент работает на Вас, выступая таким рычагом, увеличивающим ваш вклад.
Но он работает и против, когда Вы берете кредиты, например.
В принципе существуют программы, которые позволяют считать сложные проценты и связанные с ними формулы аннуитетов (аннуитетом считается ряд платежей, которые одинаковы (или меняются по закономерности) и отстоят друг от друга на одинаковый период времени, аннуитетом считается и пример с накоплением 3000 руб. в месяц выше и ежемесячная равная выплата по кредиту в течении времени).
Вы сами можете попробовать, я пользуюсь вот такой программой для iPad, она бесплатная, там у них есть варианты и для Android.
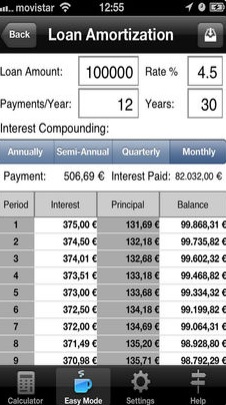
На рисунке показан пример расчета размера выплат по кредиту с использованием данной программы.
Там же можно будет попробовать и другие финансовые расчеты провести, например, подсчитать сложные проценты и аннуитеты.
Пробуйте, главное понять сам принцип.



